文/破戒僧

　　1.前言

　　必须在开篇解释一下，工具是服务于设计目标的，

　　写作本篇的目的，只是希望能帮大家节约工作时间，减少计算量，而并非鼓吹工具的重要性（但如果有同学因此喜欢上mathematica，我还是很高兴的）；后续将整理一些常用概率、统计公式或是其它可被数值设计工作使用的基础知识。


　　2.问题

　　某游戏有一种稀有武器——屠龙刀，屠龙刀可以强化到10级(初始1级)，对应的强化规则如下：

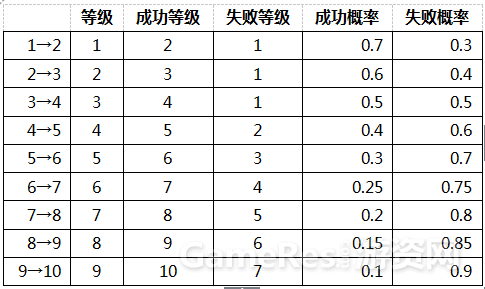
　　求得到一把+10的屠龙刀所需的强化次数

　　3.背景

　　这个问题，涉及到随机过程——马可夫过程的计算，步骤较复杂，容易出错。相对于这个计算和学习的成本，其应用场景又较单一，一般仅用于装备强化或是占星猎命。

　　但这个问题又必须有一个解决的方法，无论是用于面试还是满足项目的实际需求。通常，大部分数值策划，会选择编写VBA进行模拟运算，少部分人使用excel矩阵运算。前者通常不便于复用(少部分vba达人可以写出较通用的代码)，后者要求具备一定的数学功底。

　　于是，我推荐大家使用mathematica来解决这个问题。解答步骤仅3步，完整解答如下(详细步骤及解释见下文)：

　　4.解答步骤

　　STEP1:

　　列出状态转移矩阵：

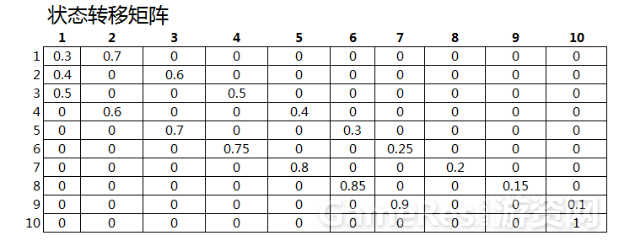
　　行的1~10代表抵达状态，第一列的1~10代表出发状态

　　如图第2行第3列的值0.7，表示的是：从状态1状态2的概率是0.7(强化成功事件)，状态1状态2的概率是0.3（强化失败事件）

　　保证每一行的概率之和为1

　　该矩阵表示每次强化只有成功和失败退回到指定等级这2种事件，可自行定义升级暴击等事件(有很小几率从1升到3之类)

　　STEP2:

　　在Mathematica中读取表格数据：

　　xlsxPath = "C:\\Users\\Administrator\\Desktop\\屠龙刀强化.xlsx";

　　m = Import[xlsxPath, "Data"][[1]][[16 ;; 25, 2 ;; 11]]

　　第一行指定excel文档的路径

　　第二行从指定excel读取数据，16;;25表示16~25行，2;;11表示2~11列(这是直接读取xlsx文件的写法，若使用mathematica link for excel加载宏，可以使用Excel[“A1:C1”]这种更好理解的语法)

　　Mathemaitca读取表格数据截图：

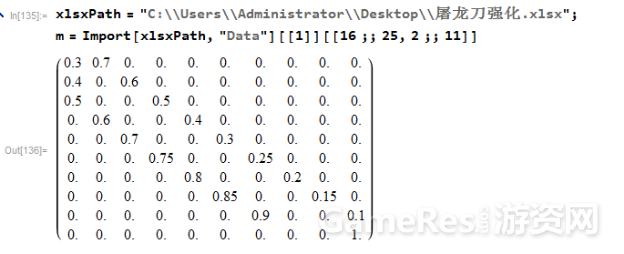
　　STEP3:

　　定义一个马尔科夫过程:

　　markovProcess = DiscreteMarkovProcess[1, m];

　　DiscreteMarkovProcess(Mathematica内置的离散马科夫过程函数)，接收2个参数：初始状态和状态转移矩阵

　　赋值这个离散马科夫过程到变量markovProcess

　　一句话的计算：

　　Mean[FirstPassageTimeDistribution[markovProcess, 10]]

　　Mean用于计算分布的期望值

　　FirstPassageTimeDistribution是求首次通过指定状态的时间分布的函数，接受2个参数：马可夫过程和最终状态（这里的最终状态是10,）

　　计算如下：

　　也可以求出在各状态的停留次数(1~9)：

　　5.问题推广：

　　在定义了马可夫过程之后，也可以进行模拟，如图模拟了10个分别强化10次的过程：

　　可以统计一下1000把屠龙刀分别强化10次后停留等级的分布：

　　也可以计算100次强化到+10的概率：

　　还可以计算每个等级不同的花费下，强化到+10的总费用，或是指定总费用，到达各等级的分布等等，有兴趣的同学可以自行研究。